Ссылка на задачу: https://leetcode.com/problems/minimum-number-of-operations-to-move-all-balls-to-each-box/description/
Имеется n коробок. На вход задана бинарная строка boxes (состоит только из 0 и 1) длины n, где boxes[i] равен ‘0’ в том случае, если i-тая коробка пустая, и равен ‘1’, если i-тая коробока содержит один мяч.
За одну операцию можно переместить мяч из текущей коробки в соседнюю. Коробки i и j считаются соседними, если abs(i - j) == 1. Обратите внимание, что после этого в некоторых коробках может оказаться более одного мяча.
Необходимо вернуть массив answer размера n такой, в котором answer[i] представляет собой минимальное количество операций, необходимое для того, чтобы переместить все остальные мячи в i-тую коробку.
Каждый answer[i] рассчитывается с учетом начального состояния коробок.
Input: “110”
Output: [1,1,3]
Объяснение:
Нулевой индекс: нужно переместить только один мяч из корбки с индексом 1, это можно сделать всего за одну операцию (коробки соседние)
Индекс 1: нужно переместить только один мяч из коробки с индексом 0, это тоже можно сделать всего за одну операцию
Индекс 2: нужно переместить два мяча (с индексами 0 и 1 соответственно); для перемещения первого потребуется две операции (из 0-ой позиции в 1-ую и из 1-ой в 2-ую), а для перемещения второго - одна операция (из 1-ой позиции сразу во 2-ую); результирующее количество операций - это 2 + 1, то есть 3
Input: “001011”
Output: [11,8,5,4,3,4]
Объяснение:
Нулевой индекс: необходимо переместить мячи с позициями 2, 4 и 5; мяч с индексом 2 может быть премещен за 2 операции, с индексом 4 - за 4 операции, с индексом 5 - за 5 операций; результат - 2 + 4 + 5, то есть 11
Смысл тот же
…
n == boxes.length
1 <= n <= 2000
boxes[i] может быть либо ‘0’, либо ‘1’
Данный способ подразумевает решение «в лоб». Необходимо пробежаться по всему массиву boxes целиком и ответить на вопрос, какое минимальное количество операций требуется, чтобы переместить в i-тую коробку все остальные мячи. «Все остальные» означает то, что нужно дополнительно итерироваться по массиву еще раз.
Так, для текущего индекса i мы проверяем все другие индексы j того же массива. Но нас интересует только те коробки, в которых есть мяч. Пустые не представляют никакого интереса. Поэтому добавляется дополнительное условие на то, что boxes[j] != ‘0’.
Сколько операций нужно для перемещения мяча из j-ой коробки в i-тую, если за раз мы имеем право перекладывать мяч только в соседнюю коробку, то есть за операцию мы можем шагнуть вдоль массива лишь раз? Ровно abs(i-j).
Индекс i может быть как меньше j, так и больше. Поэтому используется модуль разницы.
Алгоритм:
Итерируемся по всему массиву целиком (индекс i)
Для текущей внешней итерации выполняем еще одну внутреннюю итерацию по массиву (индекс j)
Если элемент boxes[j] равен ‘1’, то к i-тому элементу искомого ans прибавляем модуль разности i и j
Код:
python
class Solution:
def minOperations(self, boxes: str) -> List[int]:
ans = [0] * len(boxes)
for i in range(len(boxes)):
for j in range(len(boxes)):
if boxes[j] == '1':
ans[i] += abs(i - j)
return ansC++
class Solution {
public:
vector<int> minOperations(string boxes) {
vector<int> ans(boxes.size());
for (int i = 0; i < boxes.size(); ++i) {
for (int j = 0; j < boxes.size(); ++j) {
if (boxes[j] == '1') {
ans[i] += abs(i - j);
}
}
}
return ans;
}
};Сложность алгоритма по времени - O(N^2)
Имеем два цикла. Внешний отвечает за итерацию по массиву, внутренний - за ответ на вопрос, сколько операций требуется для текущего индекса внешнего цикла. Внутренний цикл - повторный перебор все элементов. Итак, имеем O(N*N)
Сложность алгоритма по памяти - O(1)
В данном случае не используется никаких дополнительных объектов для решения задачи. Память под сам ans в оценке не участвует, так как ans - искомый объект.
Этот способ подразумевает некоторую оптимизацию алгоритма, описанного выше. Мы все так же, как и прежде, будем итерироваться по массиву целиком, но теперь лишь два раза.
Прежде чем приступать к описанию шагов алгоритма, давайте заметим некоторый нюанс.
Допустим, что мы знаем, какое минимальное количество операций требуется для перекладки в коробку i-того индекса.
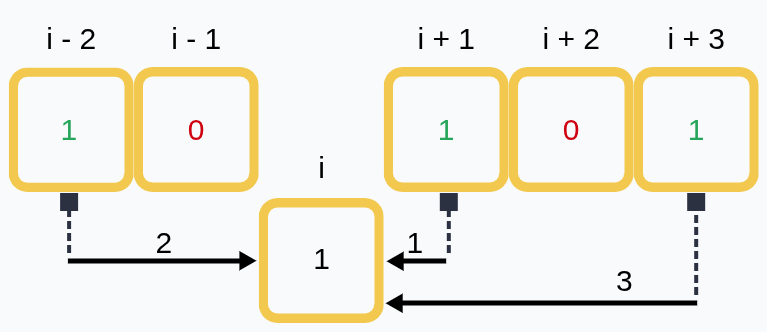
Для i-того элемента значение равно 6 (обратите внимание: нас интересуют только единицы, поэтому они отмечены зеленым цветом).
Как при этом оно поменяется, если шагнуть один раз вперед?
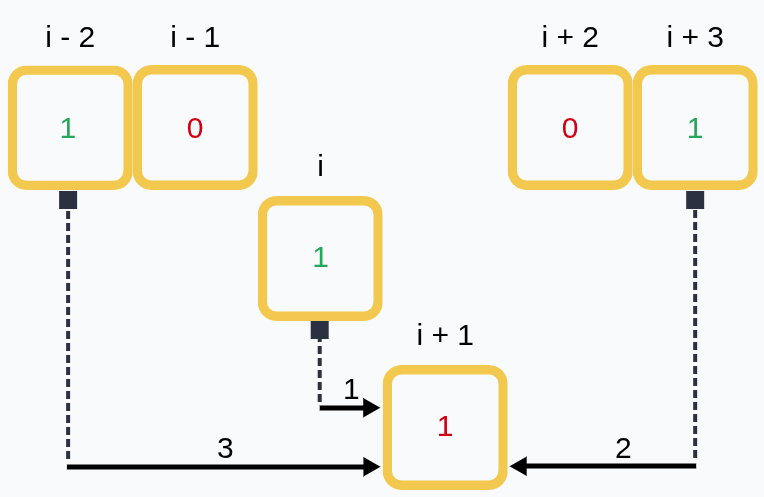
Сотрим на то, что слева от i+1. Чтобы попасть из i-2 в теперь уже i+1, потребовалось 3 шага (было 2), из появившегося i понадобился 1 шаг. Все старые значения, что находились левее, увеличились ровно на 1. Также появилась одна новая единица, которая тоже внесла свой вклад (+1).
Смотрим на то, что справа от i + 1. Во-первых, мы приблизились на шаг к i+3, поэтому значение для него стало 2 (было 3). Во-вторых, единица i+1, что для i стояла справа, теперь ушла (обратите внимание: на рисунке она теперь красная). Все старые значения, что находились правее, уменьшились ровно на 1. Также исчезла одна старая единица, которая тоже внесла свой вклад (-1).
Так, значение для ans[i + 1] = ans[i] + count_left - count_right. Дополнительно нужно выполнить ans[i + 1] -= 1.
count_left - число единиц слева
count_right - число единиц справа
Почему + count_left? Каждая единица слева от текущего элемента вносит свой вклад в размере +1. Значит суммарный вклад равен их количеству.
Почему - count_right? Каждая единица справа от текущего элемента становится ближе на 1. Суммарно их вклад уменьшается на их количество.
Зачем еще раз вычитать единицу из ans[i+1]? Сам элемент ans[i + 1] является единицей, но он не находится ни справа, ни слева, при этом его не нужно перемещать в его же коробку, он уже находится на своем месте.
Что потребовалось, чтобы определить значение ans[i+1]? Во-первых, предыдущее значение ans[i]. Во-вторых, количество единиц справа. В-третьих, количество единиц слева.
Итак, для реализации решения нужно иметь начальное значение, от которого будем отталкиваться, а также счетчики количества единиц слева и справа.
Алгоритм:
Итерируемся по всему массиву boxes целиком, начиная с индекса 1, чтобы получить начальное значение ans[0] и посчитать количество единиц справа
Иницаилизуем счетчик количества единиц слева нулем и начинаем повторную итерацию по массиву boxes с индекса 1
Проверяем, если предыдущий элемент boxes был ‘1’, то инкрементируем счетчик единиц слева
Проверяем, если i-тый элемент boxes равен ‘1’, то декрментируем счетчик единиц справа
Определяем ans[i] как ans[i - 1] + счетчик слева - счетчик справа
Дополнительно вычитаем 1 из ans[i], если i-тый элемент boxes равен ‘1’
Код:
python
class Solution:
def minOperations(self, boxes: str) -> List[int]:
n = len(boxes)
ans = [0] * n
count_ones_right = 0
# time: O(N)
for i in range(1, n):
ans[0] += int(boxes[i]) * i
if boxes[i] == '1':
count_ones_right += 1
count_ones_left = 0
# time: O(N)
for i in range(1, n):
if boxes[i - 1] == '1':
count_ones_left += 1
if boxes[i] == '1':
count_ones_right -= 1
ans[i] = ans[i - 1] - count_ones_right + count_ones_left
if boxes[i] == '1':
ans[i] -= 1
return ansC++
class Solution {
public:
vector<int> minOperations(string boxes) {
const int n = boxes.size();
vector<int> ans(n);
int count_ones_right = 0;
// time: O(N)
for (int i = 1; i < n; ++i) {
ans[0] += (boxes[i] - '0') * i;
if (boxes[i] == '1') {
count_ones_right += 1;
}
}
int count_ones_left = 0;
// time: O(N)
for (int i = 1; i < n; ++i) {
if (boxes[i - 1] == '1') {
count_ones_left += 1;
}
if (boxes[i] == '1') {
count_ones_right -= 1;
}
ans[i] = ans[i - 1] - count_ones_right + count_ones_left;
if (boxes[i] == '1') {
ans[i] -= 1;
}
}
return ans;
}
};Сложность алгоритма по времени - O(N)
В данном случае нам потребовалось всего два прохода по массиву boxes, значит сложность - O(N + N), то есть O(N).
Сложность алгоритма по памяти - O(1)
Дополнительные переменные - два счетчика, количество выделяемой под них памяти не зависит от размера входных параметров, поэтому сложность тут O(1).