Ссылка на задачу: https://leetcode.com/problems/number-of-good-pairs/description/
Дан массив целых чисел nums. Необходимо найти количество хороших пар.
Пара (i, j) является хорошей, если nums[i] == nums[j] и i < j.
Input:
| 1 | 2 | 3 | 1 | 1 | 3 |
|---|
Output: 4
Объяснение: всего 4 хороших пары: (0,3), (0,4), (3,4) и (2,5)
Input:
| 1 | 1 | 1 | 1 |
|---|
Output: 6
Объяснение: всего 6 хороших пар, так как каждая пара i < j хорошая
Input:
| 1 | 2 | 3 |
|---|
Output: 0
Объяснение: нет ни одного значения, встречающегося более 1 раза
1 <= nums.length <= 1000
1 <= nums[i] <= 100
Решение “в лоб”. Мы можем пробежаться по всему массиву целиком и для каждого индекса i использовать дополнительный цикл от i+1 до конца массива. Именно от i+1, потому что в соответствии с ограничением i < j. Во внутреннем цикле достаточно проверить, если nums[i] == nums[j], то счетчик хороших пар инкрементируется.
Алгоритм:
Итерируемся по всему массиву целиком (внешний цикл)
Для текущего элемента делаем дополнительную итерацию от следующего индекса до конца массива (внутренний цикл)
Проверяем условие равенства двух элементов (из внешнего цикла и внутреннего); в случае равенства инкрементируем счетчки хороших пар
Код:
python
class Solution:
def numIdenticalPairs(self, nums: List[int]) -> int:
ans = 0
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
if nums[i] == nums[j]:
ans += 1
return ansC++
class Solution {
public:
int numIdenticalPairs(vector<int>& nums) {
int ans = 0;
for (int i = 0; i < nums.size(); ++i) {
for (int j = i + 1; j < nums.size(); ++j) {
if (nums[i] == nums[j]) {
++ans;
}
}
}
return ans;
}
};Сложность алгоритма по времени - O(N^2)
Имеем два цикла: внешний по всем элементам O(N) и внутри каждой из итераций внешнего цикла еще внутренний, тоже O(N). Получается O(N*N).
Сложность алгоритма по памяти - O(1)
В данном решении нет никаких дополнительных объектов, под которые выделяется память.
Условие i < j дает возможность оптимизировать алгоритм, используя хэш-таблицу. Алгоритм все так же будет подразумевать итерацию по всему массиву целиком, но вместо того, чтобы для текущего элемента (индекс i) проверять все оставшиеся и находящиеся впереди (индекс j), мы будем проверять, а встречался ли элемент раньше или нет.
Если элемент уже встречался ранее, то необходимое условие задачи выполнено, ведь есть минимум одна пара (текущий элемент и тот/те, что уже встречались ранее). Нужно лишь понять, сколько таких пар появляется дополнительно.
Кстати говоря, все эти пары хорошие, так как мы итерируемся по массиву один и раз и строго в направлении слева-направо, то есть индексы не повторяются и j (индекс текущего элемента) всегда больше i (индекс встречаемого ранее элемента).
Взглянем на схему:
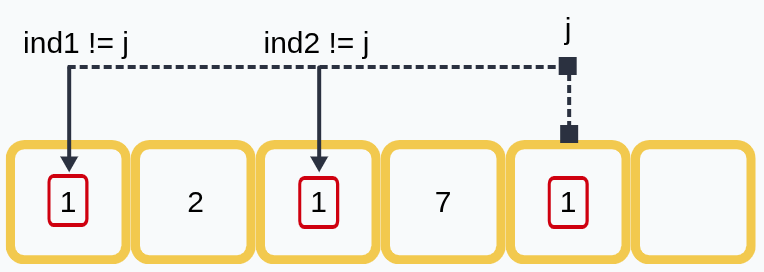
В примере для текущей единицы с индексом j ранее уже встречалось две единицы с индексами ind1 и ind2 соответственно. Текущая единица может создать дополнительно две хороших пары (по одной паре с каждой из имеющихся).
Если бы имелось 10 единиц, то текущая могла бы создать по одной хорошей паре с каждой, то есть 10 дополнительных.
Так, алгоритм сводится к тому, чтобы запоминать, какой элемент массива уже встречался и сколько раз.
Алгоритм:
Инициализировать хэш-таблицу
Итерироваться по массиву целиком
На каждой итерации проверять, встречался ли уже элемент ранее и, если встречался, то прибавлять к искомому ответу то количество, сколько раз он встречался
Добавить текущий элемент в хэш-таблицу, обновив значение его счетчика
Код:
python
class Solution(object):
def numIdenticalPairs(self, nums):
ans = 0
inspected = {}
for i in range(len(nums)):
if nums[i] in inspected:
ans += inspected[nums[i]]
else:
inspected[nums[i]] = 0
inspected[nums[i]] += 1
return ansC++
class Solution {
public:
int numIdenticalPairs(vector<int>& nums) {
unordered_map<int, int> inspected;
int ans = 0;
for (int i = 0; i < nums.size(); ++i) {
auto it = inspected.find(nums[i]);
if (it != inspected.end()) {
ans += it->second;
}
++inspected[nums[i]];
}
return ans;
}
};Сложность алгоритма по времени - O(N)
В данном случае нам достаточно одного прохода по массиву.
Сложность алгоритма по памяти - O(N)
Для реализации используется дополнительная хэш-таблица, количество элементов в которой равно длине массива.